Der Zeeman-Effekt beschreibt die Aufspaltung von Spektrallinien unter Einwirkung eines äußeren Magnetfeldes auf das emittierende Atom. Die Aufspaltung der Spektrallinien wurde erstmals von dem Physiker Pieter Zeeman 1896 bei der Untersuchung der Spektrallinien von Natrium unter dem Einfluss eines äußeren Magnetfeldes beobachtet. Die Auswirkungen des Effekts sind klein und erfordert für deren Untersuchung Spektralapparate mit sehr hoher Auflösung. Schon kurz nach der Entdeckung konnte Hendrik Antoon Lorentz den Zeeman-Effekt mit der klassischen Elektronentheorie weitgehend erklären, auch wenn erst die Quantenmechanik eine vollständige Beschreibung liefert. Im Folgenden wird die Betrachtung auf den normalen Zeeman-Effekt eingeschränkt, der nur auftritt, wenn sich der Gesamtspin aller Elektronen eines Atoms zu Null addiert. Ein von außen angelegtes Magnetfeld wirkt dann nur noch auf den Bahndrehimpuls der Elektronen.
Klassische Erklärung nach Lorentz
Im Rahmen der klassischen Theorie interpretiert man die Emission von Licht als das Resultat einer Elektronenschwingung. Das strahlende Elektron wird als linearer Oszillator betrachtet, der zufällig zu den Magnetfeldlinien des äußeren Feldes ausgerichtet ist. Die lineare Oszillation wird aufgeteilt in drei Komponenten: Komponente 1 schwingt parallel zur Feldrichtung, die Komponenten 2 und 3 schwingen kreisförmig in einer Ebene senkrecht zum Feld in umgekehrten Richtungen (siehe Abb. 1). Überlagert man diese drei Schwingungen wieder, so erhält man wieder die ursprüngliche lineare Schwingung. Ohne das äußere Feld ist die Frequenz aller drei Oszillatoren identisch mit der Frequenz $\omega_0$ des Ausgangselektrons.
Durch das äußere Feld erfahren die Komponenten jedoch verschiedene Kräfte:
- Komponente 1 erfährt keine Kraft, die Frequenz bleibt konstant. Der Oszillator emittiert linear polarisiertes Licht mit Polarisationsebene parallel zur Feldrichtung.
- Die Komponenten 2 und 3 werden beschleunigt oder abgebremst um den Betrag $$ \Delta \omega=\frac{e}{2m_e}B_0 = \frac{\mu_B}{\hbar}B_0 $$ und emittieren somit zirkular polarisiertes Licht der Frequenz $\omega_0 \pm \Delta \omega $.
Klassisch lässt sich dies leicht aus den Bewegungsgleichungen des Elektrons in kartesischen Koordinaten erkennen:
$$ \begin{align} m\ddot{x} + m\omega^2_0x - eB\dot{y} & = 0 \\ m\ddot{y} + m\omega^2_0y + eB\dot{x} & = 0 \\ m\ddot{z} + m\omega^2_0z & = 0 \end{align} $$
die mit der Substitution $u = x+iy$ und $v = x-iy$ unter der Voraussetzung $e B_0 /2m \ll \omega_0$ durch
$$ \begin{align*} u & = u_0\exp\left(i(\omega_0 - eB_0/2m)t\right)\\ v & = v_0\exp\left(i(\omega_0 + eB_0/2m)t\right)\\ z & = z_0\exp\left(i\omega_0z\right) \end{align*} $$
gelöst werden.
Zusammenfassend erhält man also eine unverschobene, linear polarisierte Komponente mit Schwingungsebene parallel zum Magnetfeld, die $\pi$-Komponente genannte wird und zwei verschobene, zirkular polarisierte Komponenten, die mit $\sigma_+ $ und $\sigma_-$ bezeichnet werden. Für die $\pi$-Komponente erwartet man als Hertz’schen Dipol keine Abstrahlung in Magnetfeldrichtung und die $\sigma_\pm$-Komponenten sollten in Beobachtungsrichtung senkrecht zum Magnetfeld linear polarisiert sein.
Semiklassische Erklärung
Nach dem Bohrschen Atommodell erzeugt das auf einer Kreisbahn um den Kern laufende Elektron ein magnetisches Moment $\mu$, das proportional zu seinem Drehimpuls ist. Der Drehimpuls steht senkrecht auf der Bahnebene und definiert damit die Lage der Bahn im Raum. Nach dem ersten Bohrschen Postulat können nur diskrete Bahnen eingenommen werden, d. h. der Drehimpuls muß gequantelt sein.
Der klassische Drehimpuls wird durch die gequantelte Größe $\vec{L}=\sqrt{l(l+1)}\hbar$ mit der Drehimpulsquantenzahl $l = 0,1,\ldots,(n - 1)$ ersetzt und erzeugt das Bahnmoment
$$ \vec{\mu}_l=\mu_B\dfrac{\vec{L}}{\hbar} $$
mit dem Bohrschen Magneton $\mu_B=e\hbar/2m$. Ein weiterer magnetischer Beitrag entsteht durch den Spin $\vec{S}$ des Elektrons. Wir betrachten hier jedoch nur Atome mit abgesättigtem Spin $\vec{S} = 0$. Ihr magnetisches Moment wird nur durch den Bahndrehimpuls erzeugt. Für die Messung ist wichtig, daß $\vec{L}$ selbst nicht ermittelt werden kann, sondern nur seine Projektion $L_z$ auf eine ausgezeichnete Achse, die durch ein externes Magnetfeld (in z-Richtung) gegeben ist
$$ L_z = m_l\hbar \quad\text{mit}\quad m_l = -l,\ldots,{+l} $$
wobei $m_l$ die magnetische Quantenzahl bezeichnet. Dies bedeutet, der Drehimpuls kann sich nur in bestimmten Winkeln zum Magnetfeld einstellen - dieses Verhalten bezeichnet man auch als Richtungsquantelung.
Durch die magnetische Quantenzahl ist die Ausrichtung in einem externen Magnetfeld gegeben, die Ausrichtung des magnetischen Moments bestimmt aber dessen Energie
$$ E_{mag} = - \vec{\mu}_L \cdot \vec{B} $$
im $B$-Feld. Werden Atome in ein externes Magnetfeld gebracht, führt dies also zu einer Aufspaltung und Verschiebung der Energieniveaus, je nachdem wie sich das magnetische Moment zum $B$-Feld einstellt. Dadurch kommt zur Energie $E_n$ des Elektrons im Coulomb-Feld zusätzlich ein Korrekturterm
$$ E_{n,l,{m_l}}=E_n + \mu_B m_l B $$
Ohne Magnetfeld ist die Energie $E_n$ des Atoms also durch die Hauptquantenzahl $n$ gegeben, unabhängig von $m_l$, d. h. der Zustand ist entartet. Erst durch das Magnetfeld entsteht eine Vorzugsrichtung im Raum und die Entartung der Zustände wird aufgehoben. Dabei spaltet jedes ungestörte Niveau in ein Multiplett aus $(2l+1)$ äquidistanten Niveaus auf mit dem Abstand $\Delta E = \mu_B B$, die so genannte Zeeman-Aufspaltung.
Quantenmechanische Erklärung
Der Einfluss eines äußeren Feldes auf die Energieeigenwerte lässt sich allerdings auch formal quantenmechanisch ableiten.
Mit der bekannten Hamilton-Funktion des Elektrons ($q = -e$) im externen Magnetfeld
$$ H = \frac{1}{2m_e}\left(\vec{p} + \frac{e}{c}\vec{A}\right)^2 + V(\vec{x}) $$
folgt nach korrespondenzmäßigem Übergang $\vec{p} = -i\hbar\nabla$ für den Hamilton-Operator
$$ \hat{H}\psi = \frac{1}{2m_e}\left[\left(-\hbar^2\laplacian + \frac{e^2}{c^2}\vec{A^2}\right)\psi +\frac{e\hbar}{ic}\left(\nabla\cdot(\vec{A}\psi ) + \vec{A}\cdot\nabla\psi\right)\right] + V\psi $$
Mit den Regeln zur Divergenzbildung und aufgrund der Coulomb-Eichung $\nabla\cdot\vec{A} = 0$ erhalten wir für den Hamilton-Operator
$$ \hat{H} = \hat{H}_0 + \hat{H}’ + \hat{V}_Z $$
mit dem ungestörten Hamilton-Operator
$$ \begin{align} \hat{H}_0 & = - \frac{\hbar^2}{2m_e}\laplacian + V(\vec{x}), \\ \hat{H}’ & = \frac{e^2}{2m_ec^2}\vec{A}^2 \end{align} $$
und dem Zeeman-Störoperator
$$ \hat{V}_Z = - \frac{ie\hbar}{m_ec}\vec{A}\cdot\nabla $$
Durch Einsetzen des Vektorpotentials $\vec{A} = \frac{1}{2}\vec{B}\times\vec{r}$ in den Zeeman-Störoperator erhält man mit $\vec{p} = -i\hbar\nabla$:
$$ \vec{V}_Z = -\frac{e}{2m_ec}\left(\vec{r}\times i\hbar\nabla\right)\cdot\vec{B} = \frac{e}{2m_ec}\left(\vec{r}\times\vec{p}\right)\cdot\vec{B} = \frac{e}{2m_ec}\vec{L}\cdot\vec{B}_{ext} $$
mit dem Bahndrehimpulsoperator $\hat{\vec{L}} = \hat{\vec{r}}\times\hat{\vec{p}}$. Mit dem magnetischen Dipolmoment des Elektrons durch die Bahnbewegung
$$ \vec{\mu}_L = -\frac{e}{2m_ec}\vec{L} $$
schreibt sich der Zeeman-Störoperator als
$$ \hat{V}_Z = -\vec{\mu}_L \cdot \vec{B}_{ext} $$
O. b. d. A. legen wir das externe Feld in Richtung der $z$-Achse und betrachten die Coulombwechselwirkung mit $V(\vec{x})$. Solange die externen Magnetfeldstärken klein sind, dürfen wir den Operator $\hat{H}’$ vernachlässigen. Damit erhalten wir für den Hamilton-Operator
$$ \hat{H} = \hat{H}_0 + \hat{V}_Z = \hat{H}_0 + \frac{eB}{2m_ec} \vec{L}_z $$
$\hat{H}_0$, $\vec{L}^2$ und $\vec{L}_z$ haben dabei das vollständige System gemeinsamer Eigenfunktionen. Die Energieeigenwerte des ungestörten Hamilton-Operators sind von $m$ unabhängig und $(2l+1)$-fach entartet.
Der Gesamt-Hamilton-Operator $\hat{H}$ ist die Summe von $\hat{H}_0$ und $\vec{L}_z$. Damit besitzt er dieselben Eigenfunktionen. Mit $\vec{L}_z = m\hbar$ sind die Energieeigenwerte des Gesamt-Hamilton-Operators dann
$$ \hat{H} = \hat{H}_0 + \frac{eB}{2m_ec}\vec{L}_z = E^{nl}_0 + \frac{eB}{2m_ec}m\hbar, $$
also
$$ E^{nlm} = E^{nl}_0 + m \mu_B B, $$
mit dem Bohrschen Magneton
$$ \mu_B = \frac{e\hbar}{2m_ec} $$
Weil $m$ alle ganzzahligen Werte von $-l$ bis $+l$ durchlaufen kann, wird unter dem Einfluss eines externen Magnetfeldes jedes Energieniveau in $(2l+1)$-äquidistante Niveaus aufgespaltet.
Bei der Absorption und Emission von Photonen durch ein Atom beobachtet man, daß die Drehimpulsquantenzahl $l$ des Atoms sich um $1$ ändert. Dies ist Folge der Drehimpulserhaltung, da das Photons selbst einen Eigendrehimpuls von $\hbar$ trägt. Die Auswahlregel für diese optischen Dipol-Übergänge sind gegeben als
$$ \Delta m = \pm1,0 \quad\vee\quad \Delta l = 1 $$
Dies lässt sich wie schon oben beschrieben klassisch ableiten.
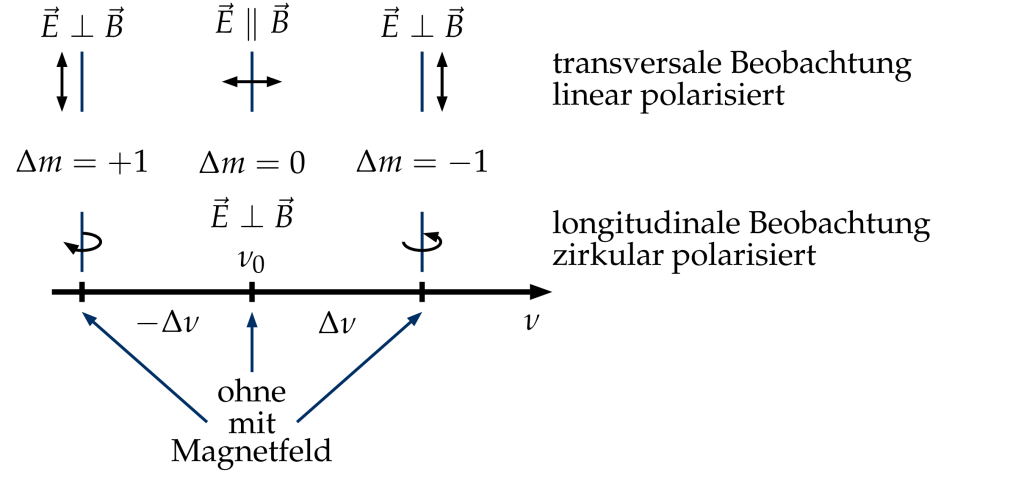
Abb. 3: Normaler Zeeman-Effekt. Aufspaltungsbild und Polarisation einer Spektrallinie mit der Mittenfrequenz $nu_0$ bei transversaler und longitudinaler Beobachtung. Die Aufspaltung ist $\Delta \nu = \mu_B \cdot B/h$Die Absorption bzw. Emission von Photonen ändert den Drehimpuls des Atoms jeweils um $\hbar$. Dementsprechend ist die Polarisation der absorbierten/emittierten Photonen unterschiedlich je nach Richtung zum Magnetfeld. Parallel zum Magnetfeld ist das Licht zirkular polarisiert, senkrecht dazu ist es linear polarisiert (siehe Abb. 3).